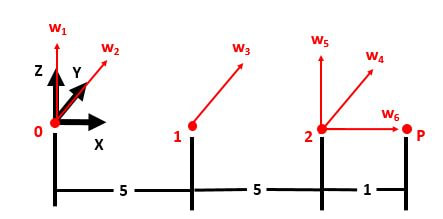
This project centers around a Matlab simulation of a 6 axis robotic manipulator. This robotic arm has 6, rotary joints: 2 at the shoulder, an elbow joint, and 3 rotary joints combined to form a wrist joint of the arm. The arm was modeled in Matlab as a stick figure model of a real arm holding a stylus. The upper and lower arm were 5 units long with a 1 unit length stylus on the end.
The algorithm that this project would be based off is called the probabilistic roadmap algorithm. This algorithm creates a roadmap of connected free configurations of the robot that is used to generate collision free paths in the physical operating space. The process that this algorithm follows begins with the random generation of configurations. In this case, each joint had its own uniform random distribution that the random joint configurations were selected from. The shoulder joints were limited in a way that the elbow of the arm never left the physical space. Using the product of exponentials forward kinematics as described above.
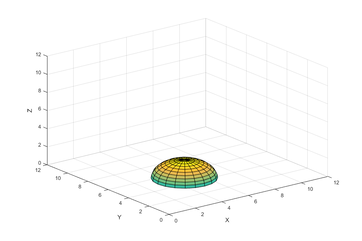
After the random configurations were generated, the configuration had to be evaluated to determine if it was collision free or not. To do this, the location of each of the four main points were calculated. The collision checking algorithm would first check that all of the four points in the arm were within the limits of the physical space above. It would then check that each of the point were in collision with the obstacle in the center of the space. This is a relatively simple process because the obstacle is a sphere with a known location. The process of determining if a point is in collision with the obstacle is as simple as comparing the distance of the point to the center of the sphere with the radius of the obstacle. If the distance between the point and the center is less than the radius of the sphere, the point must be inside of the sphere by definition. If all of the main points of the arm are collision free, the midpoints of the arm segments are evaluated in the same manner. If all of those points pass inspection, the quarter points of the segments are checked. If this configuration passes all of the collision checking tests, the joint angles of the configuration as well as the location of the stylus in the physical space are both recorded and stored.
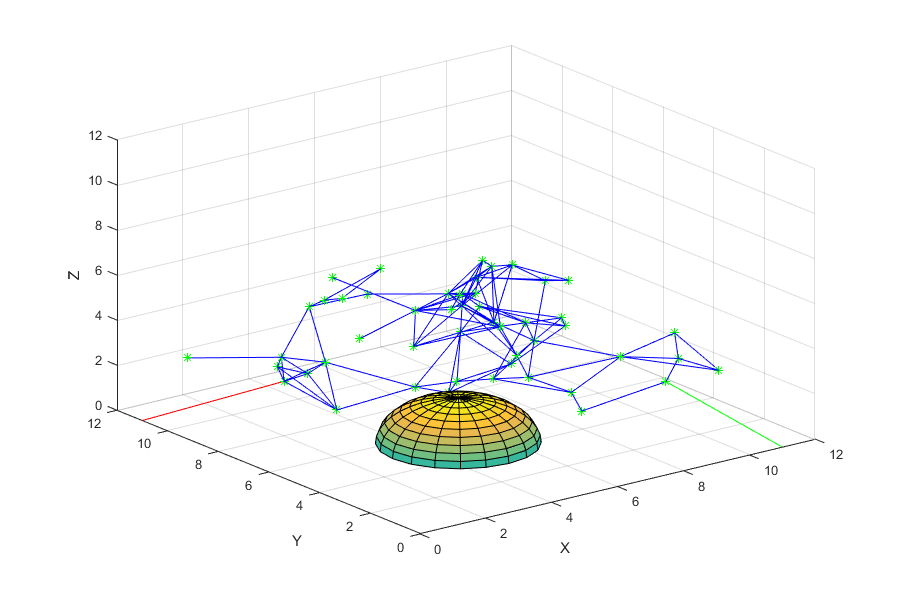
The path planner used in this algorithm is a straight line path planner. The path generated between the points is a straight line in the physical space between the two configurations. Just as the points that are generated must be checked for collisions, so do the paths between them. The paths are checked in a similar manner, starting with the middle point between the two free configuration points. If the distance between the mid point and the center of the obstacle is less than radius of the sphere, than the path would be in collision. If the midpoint passes, the quarter points are also checked. All of these paths and free configuration points are stored and plotted to form a road map.
Once the road map is generated for the space, it can be used to find a path between any two points in the physical space. In this case, only one path is being generated, but many paths could be made from the same roadmap. The first step is to connect the start and goal points with the roadmap. This is as simple as finding the nearest point to the start and goal points in the roadmap. These paths are stored as the beginning and end of the eventual path that the arm takes.
This, however is not a foolproof system. This simple system can cause the path to get stuck in dead end path where the only way to reach the goal is to retrace the path back to another path that can reach the goal. The algorithm will always start by following the path that follows the connected node that is closest to the goal, keeping track of the nodes in the path. If there are no connected nodes that have not already been traveled to on that path, that node is labeled as a dead end node. The search process than restarts avoiding the dead end nodes until the goal or another dead end node is reached. This repetitive cycle of trying to find the shortest path while avoiding dead end nodes will eventually find a path if there exists one.
| | |
This project was relatively simple as it had a 1 month timeline, but could be improved for more powerful path finding in the same system. By using a more detailed path planner and edge finder that are based on the joint angles instead of the physical distance of the nodes and a straight line between them, the simulation can more realistically model the motions of a physical robotic arm. As you can see a lot of the free configurations tend to be in the middle of the space as it is more probable to find free configurations in this space based on the joint distributions. This could be adjusted by making non uniform distributions or using a resampling process based off of the location of the points or some other method to change the distribution of the nodes.

 RSS Feed
RSS Feed
